ESTRUCTURA CRISTALINA EN MATERIALES
INTRODUCCIÓN
La mayoría de los materiales sólidos no metálicos con los que uno a diario esta en contacto, encuentra que no hay diferencia característica entre su forma externa y la de casi todos los objetos metálicos. De aquí que resulte bastante sorprendente para la mayoría de la gente saber que los materiales metálicos poseen una estructura cristalina, mientras que materiales como la madera, plásticos, papel, vidrio y otros no la poseen, éste tipo de materiales tienen un arreglo al azar en sus partículas de manera que logran rigidez a la temperatura ambiente.
Los sólidos se pueden clasificar teniendo en cuenta el arreglo interno de sus partículas, en amorfos y cristalinos.
Se puede decir que un sólido es un material que posee forma y volumen definidos y que es una sustancia constituida por átomos metálicos, átomos no metálicos, iones ó moléculas.
Muchas de las propiedades de los metales tales como la densidad, dureza, punto de fusión, conductividad eléctrica y calorífica están relacionadas con la estructura cristalina y también con el enlace metálico. Sin embargo, ninguna depende tanto de la estructura cristalina como las propiedades mecánicas tales como la maleabilidad, ductilidad, resistencia a la tensión, temple y capacidad de hacer aleaciones.
SÓLIDOS AMORFOS
Son todos aquellos sólidos en los cuales sus partículas constituyentes presentan atracciones lo suficientemente eficaces como para impedir que la sustancia fluya, resultando una estructura rígida y más o menos dura.
No presentan una disposición interna ordenada por lo tanto no tienen ningún patrón determinado. También se les denomina vidrios ó líquidos sobreenfriados.
A temperaturas altas los amorfos se transforman en líquidos y sus partículas constituyentes tienen libertad de movimiento, al disminuir lentamente la temperatura, la energía cinética de las partículas se va haciendo tan baja que se puede producir un acomodamiento entre ellas; pero si el enfriamiento se produce rápidamente y por debajo del punto de fusión (sobreenfiramento), se origina, como resultado de las menores vibraciones, una contracción térmica que no permite el ordenamiento de las partículas aumentando la viscosidad que ya no es posible apreciar flujo y la sustancia adquiere las características de un sólido: rigidez, dureza, forma y volumen definidos, etc. Como ejemplos cabe resaltar: el asfalto, ceras, la brea, vidrio y la mayoría de los polímeros.
Cuando un sólido amorfo se quiebra produce caras y bordes irregulares y al fundirse lo hace en un rango de temperaturas cambiando lentamente del estado sólido al estado líquido.
SÓLIDOS CRISTALINOS Y REDES DE BRAVAIS
Los sólidos cristalinos están constituidos por minúsculos cristales individuales cada uno con forma geométrica y poseen la característica de que al romperse producen caras y planos definidos, al igual presentan puntos de fusión definidos. Como ejemplos podemos destacar: el NaCl, la sacarosa, metales y aleaciones, y también algunos cerámicos.
Los átomos o iones de un sólido se ordenan en una disposición que se repite en tres dimensiones, forman un sólido del que se dice tiene una estructura cristalina, se dice también que es un sólido cristalino o un material cristalino.
| Punto reticular: ión, átomo o moléculaque se repite infinitamente | 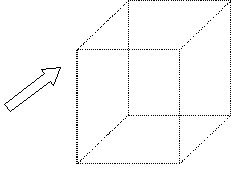 figura 1 figura 1 |
| Líneas rectas imaginarias que forman laCeldilla unidad | 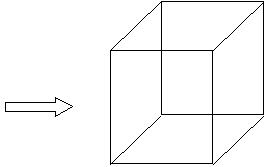 figura 2 figura 2 |
| El patrón se repite en el espacio yForma el retículo cristalino | 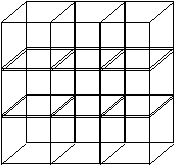 figura 3 figura 3 |
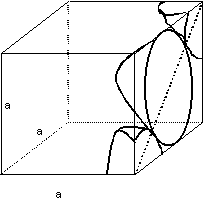
El tamaño y la forma de la celda unidad pueden describirse por tres vectores reticulares a, b, c y por ángulos entre las caras y la longitud relativa de las aristas, denominados parámetros de red, constantes de red o ejes cristalográficos.
a, b, c : longitud de las aristas correspondientes a los ejes coordenados X, Y,Z.
a , b , g : ángulos entre las aristas.
 figura 4
figura 4
La importancia en la ingeniería de la estructura física de los materiales sólidos depende primordialmente de la disposición de los átomos, iones o moléculas que constituyen el sólido y de las fuerzas de enlace entre ellos.
Asignando valores específicos para las longitudes axiales y los ángulos intereaxiales, se pueden construir diferentes tipos de celda unidad. Los cristalógrafos han mostrado que son necesarias sólo siete tipos de diferentes de celda unidad para crear todas las redes puntuales, estos sistemas cristalinos son: el Cúbico, el Tetragonal, el Ortorrómbico, el Romboédrico, el Hexagonal, el Monoclínico y el Triclínico. La mayor parte de los sistemas cristalinos presentan variaciones de la celda unidad básica. A.J. Bravais mostró que 14 celdas unidad estándar podían describir todas las estructuras reticulares posibles. Hay cuatro tipos básicos de celdas unidad (1) Sencilla, (2) Centrada en el Cuerpo, (3) Centrada en las Caras, y (4) Centrada en la Base.
En el Sistema Cúbico hay tres tipos de celda unidad: cúbica sencilla, cúbica centrada en el cuerpo y cúbica centrada en las caras. En el Sistema Ortorrómbico hay están representados los cuatro tipos. En el Sistema Tetragonal hay solo dos: sencilla y centrada en el cuerpo. La celda unidad tetragonal centrada en las caras parece que falta, pero se puede formar a partir de cuatro celdas unidad tetragonales centradas en el cuerpo. El Sistema Monoclínico tiene celdas unidad sencilla y centrada en la base, y los Sistemas Romboédrico, Hexagonal y Triclínico tienen sólo una celda unidad.
PRINCIPALES ESTRUCTURAS CRISTALINAS METÁLICAS
La mayoría de los metales elementales (90%) cristalizan en tres estructuras cristalinas densamente empaquetadas: cúbica centrada en las caras FCC, hexagonal compacta HCP y cúbica centrada en el cuerpo BCC debido a que se libera energía a medida que los átomos se aproximan y se enlazan cada vez más estrechamente entre sí. Por lo tanto dichas estructuras densamente empaquetadas se encuentran en disposiciones u ordenamientos de energía cada vez más baja y estable.
Ejemplo
¿ Cuántas celdas unidad hay aproximadamente en el Fe puro BCC si las aristas de la celda estuvieran alineadas arista con arista en 1 mm, si a temperatura ambiente la arista es igual a 0.287 X 10-9 nm ?
Estructura Cristalina Cúbica Centrada en el Cuerpo BCC
En esta celda unidad las esferas sólidas representan los centros donde los átomos están localizados e indican sus posiciones relativas. En esta celda unidad el átomo central esta rodeado de 8 vecinos más cercanos y se dice que tiene por lo tanto un número de coordinación de 8. Cada una de estas celdas unidad tiene el equivalente de 2 átomos por celda unidad. Un átomo completo esta localizado en el centro de la celda unidad, y un octavo de esfera esta localizado en cada vértice de la celda unidad, haciendo el equivalente de otro átomo. De este modo, hay un total de 1 (en el centro) + 8 x 1/8 (en los vértices) = 2 átomos por celda unidad.
Los átomos en este tipo de celdas contactan entre sí a través de la diagonal del cubo, y la relación entre la longitud de la cara del cubo a y el radio atómico R es:
Si los átomos en la celda BCC se consideran esféricos, el factor de empaquetamiento atómico (APF) puede hallarse empleando la siguiente expresión:
El APF de esta celda es 0.68, es decir, el 68% del volumen de la celda esta ocupado por átomos y el 32% restante en espacio vacío. El cristal BCC no es una estructura totalmente compacta, ya que los átomos aún podrían situarse más juntos. Muchos metales como el Cromo, Hierro, Wolframio, Molibdeno y Vanadio tienen estructura cristalina BCC.
Estructura Cristalina Cúbica Centrada en las Caras FCC. En esta celda hay un punto reticular en cada vértice del cubo y otro en el centro de cada cara del cubo. El modelo de esferas sólidas indica que los átomos de esta estructura están unidos del modo más compacto posible. El APF de esta estructura de empaquetamiento compacto es 0.74.
Esta celda tiene el equivalente a cuatro átomos por celda unidad. Un octavo de átomo en cada vértice (8 x 1/8=1) y seis medios átomos en el medio (1/2 x 6= 3).
Los átomos en la celda FCC contactan entre sí a lo largo de la diagonal de la cara del cubo, de tal forma que la relación entre la longitud de la cara del cubo y el radio atómico es:
Metales como el Aluminio, el Cobre, el Plomo, el Níquel y el Hierro a temperaturas elevadas (912 a 1394°C) cristalizan según la estructura FCC.
Ejemplo
El Cu posee una estructura FCC y un radio atómico de 0.1278 nm y considerando que los átomos son esferas sólidas que contactan a lo largo de las diagonales de la celdilla unidad FCC. ¿ Cuál es el valor teórico de la densidad del Cu ?
Masa atómica del Cu=63.54 g/mol
1/8 * 8= 1 átomo½ * 6= 3 átomo
a 4 átomos en la celda FCC | figura 5 |
Parámetro de Red:
Volumen de la celda:
V=a3 = (0.361nm)3 =0.047nm3x(1X10-9m)3 = 4.7 x 10-29 m3
Masa de los átomos de Cu en la celda:
Densidad Volumétrica:
El valor tabulado experimentalmente es de 8.96  , la diferencia se debe a que los átomos no son esferas perfectas, a la ausencia de átomos en las posiciones atómicas, a defectos en la red, etc.
, la diferencia se debe a que los átomos no son esferas perfectas, a la ausencia de átomos en las posiciones atómicas, a defectos en la red, etc. Estructura Cristalina Hexagonal Compacta HCP
Los metales no cristalizan en la estructura hexagonal sencilla porque el APF es demasiado bajo. El APF es 0.74 ya que los átomos están empaquetados de un modo lo más cercano posible. Cada átomo esta rodeado de otros 12 átomos y por tanto su número de coordinación es 12.
La celda HCP posee 6 átomos, tres forman un triángulo en la capa intermedia, existen 6*1/6 secciones de átomos localizados en las capas de arriba y de abajo, haciendo un equivalente a 2 átomos más, finalmente existen 2 mitades de átomo en el centro de ambas capas superior e inferior, haciendo el equivalente de un átomo más.
La relación c/a de una estructura cristalina HCP ideal es de 1.633 que indica esferas uniformes tan próximas como sea posible. Los metales Cinc, Cadmio poseen una relación c/a más alta que la ideal, lo que indica que los átomos en estas estructuras están ligeramente elongados a lo largo del eje c en la celda unidad HCP. Los metales como el Titanio, Berilio, Magnesio Y Circonio entre otros tienen relaciones c/a menores que la ideal. Por tanto en estos metales los átomos están comprimidos a lo largo de la dirección del eje c.
ÍNDICES DE MILLER
Celdas Cúbicas. Los índices de Miller de un plano cristalino están definidos como los recíprocos de las intersecciones que el plano determina con los ejes x, y, z de los tres lados no paralelos del cubo unitario. Las aristas de una celda cúbica unitaria representan longitudes unitarias y las intersecciones de los planos de una red se miden en base a estas longitudes unitarias.
El procedimiento para determinar los índices de Miller para un plano de un cristal cúbico es el siguiente:
Escoger un plano que no pase por el origen en (0,0,0)
Determinar las intersecciones del plano en base a los ejes x, y, z cristalográficos para un cubo unitario. Estas intersecciones pueden ser fraccionarias.
Construir los recíprocos de las intersecciones.
Despejar fracciones y determinar el conjunto más pequeño de números enteros que estén en la misma razón de las intersecciones. Estos números enteros son los índices de Miller de un plano cristalográfico y se encierran entre paréntesis sin usar comas. La notación (hkl) se emplea para indicar los índices de Miller en sentido general, donde h, k, y l son los índices de Miller para un plano de un cristal cúbico de ejes x, y, y z respectivamente.
Ejemplos
figura 6
Las intersecciones del primer plano son 1, 1, y los recíprocos de estos números son 1, 1, 0 no involucran fracciones, siendo los índices de Miller (1 1 0).
y los recíprocos de estos números son 1, 1, 0 no involucran fracciones, siendo los índices de Miller (1 1 0). Para la segunda figura, las intersecciones son: 1,  ,
,  a los ejes x, y, z respectivamente, por lo tanto los recíprocos son: 1, 0, 0. Los índices de Miller para este plano son: (1 0 0 ).
a los ejes x, y, z respectivamente, por lo tanto los recíprocos son: 1, 0, 0. Los índices de Miller para este plano son: (1 0 0 ). Finalmente, el tercer plano, tiene las intersecciones 1, 1, 1 que nos dan un índice de Miller (1 1 1).
Si se considera que el plano cristalino pasa por el origen de manera que uno ó más cortes se hacen cero, el plano ha de ser desplazado a una posición equivalente en la misma celda unitaria de modo que el plano permanezca paralelo al original. Esto es posible porque todos los planos paralelos equidistantes son indicados con los mismos índices de Miller.
Si grupos de planos de redes equivalentes están relacionados por la simetría del sistema cristalino, se llaman familia de planos, y los índices de una familia de planos son encerrados entre llaves. Por ejemplo, los índices de Miller de los planos de la superficie del cubo (100) (010) y (001) se designan colectivamente como una familia con la notación {100}.
Una importante relación sólo para el sistema cúbico es que los índices de una dirección perpendicular a un plano de un cristal son los mismos que los índices de Miller para ese plano. Por ejemplo, la dirección [100] es perpendicular al plano cristalino (100).
Celda HCP. Se identifican empleando cuatro índices en vez de tres, se denominan índices Miller-Bravais, son representados por las letras h, k, i, l y encerrados entre paréntesis (h, k, i, l). Estos índices hexagonales están basados en un sistema coordenado de cuatro ejes, tres ejes básicos a1,a2,a3 que forman 120° entre sí, el cuarto eje o eje c es el eje vertical y está localizado en el centro de la celdilla unidad (Ver figura). La unidad a de medida a lo largo de los ejes a1,a2,a3 es la distancia entre los átomos. La unidad de medida a lo largo del eje c es la altura de la celdilla unidad. Los recíprocos de las intersecciones que un plano determina con los ejes a1,a2,a3 proporcionan los índices h, k e i mientras que el reciproco de la intersección con el eje c da el índice l.
figura 7
Los planos basales de la celdilla unidad HCP son muy importantes para esta celdilla, el plano basal de la parte superior es paralelo a los ejes a1,a2,a3 , las intersecciones de este plano con estos ejes serán todas de valor infinito. Así, a1 = a2= a3 = . El eje c, sin embargo, es único puesto que el plano basal superior intersecciona con el eje c a una distancia unidad. Tomando los recíprocos de estas intersecciones tenemos los índices de Miller-Bravais para el plano basal HCP. Así, h=0, K=0, i=0, l=1. El plano basal es, por tanto, un plano (0001).
. El eje c, sin embargo, es único puesto que el plano basal superior intersecciona con el eje c a una distancia unidad. Tomando los recíprocos de estas intersecciones tenemos los índices de Miller-Bravais para el plano basal HCP. Así, h=0, K=0, i=0, l=1. El plano basal es, por tanto, un plano (0001). Las direcciones en las celdas unitarias HCP se indican por cuatro índices [u,v,t,w]. Son vectores reticulares en las direcciones a1,a2,a3 respectivamente y el índice w es un vector reticular en la dirección c.
SISTEMAS DE DESLIZAMIENTO
Un sistema de deslizamiento es la combinación de un plano y una dirección que se halla sobre el plano a lo largo del cual se produce el deslizamiento.
El Mecanismo de deslizamiento puede definirse como el movimiento paralelo de dos regiones cristalinas adyacentes, una respecto a la otra, a través de algún plano (o planos).
El deslizamiento no se produce sobre un plano solamente, sino sobre pequeñas regiones de planos paralelos llamados bandas de deslizamiento o líneas de deslizamiento, dependiendo de sus espesores. Puesto que todas las líneas de deslizamiento está en grupos paralelos dentro de cada monocristal (cada grano), deben corresponder a una misma familia de planos (hkl) ocupados del grano particular. A partir de mediciones sobre especímenes de monocristales de orientaciones conocidas se puede determinar 1) los planos sobre los cuales se produce el deslizamiento y 2) la dirección de deslizamiento dentro de estos planos. Tales experimentos han revelado que en las estructuras FCC el deslizamiento siempre se produce sobre los planos {111} pero solamente en las direcciones <110>. Esto significa que si se produce el deslizamiento sobre el plano (111) será en alguna de las tres direcciones ± [101], ±[110], ±[011].
Los cristales FCC poseen 12 sistemas de deslizamiento debido a que tienen cuatro grupos {111} y con tres direcciones <110> en cada una.
En otras estructuras de cristales metálicos, los sistemas de deslizamiento tienen más variabilidad. En los metales BCC las líneas de deslizamiento tienen una apariencia ondulada. En estos cristales el deslizamiento se produce predominantemente en los sistemas {110} <111> y la apariencia ondulada se debe aparentemente a deslizamiento simultáneo sobre los otros dos sistemas de planos {211} y {321} . En cristales HCP reales, la relación c/a no es igual al valor ideal de 1.633 del modelo de esfera dura. Para los metales c/a > 1.633 hay alguna preferencia para el deslizamiento sobre el plano basal, <1120>(0001), mientras que para aquellos metales con c/a < 1.633 los sistemas de deslizamiento preferidos son los otros dos.
Estructura | Dirección de Deslizamiento | Planos de Deslizamiento | Ejemplos |
FCC | <110> | {111} | Cu, Al, Ni, Pb, Au, Ag, Fe |
BCC | <111> | {110} | Fe, W, Mo, Latón, Nb, Ta |
BCC | <111> | {210} | Fe, Mo, W, Na |
BCC | <111> | {321} | Fe, K |
HCP | <1120> | (0001) | Cd, Zn, Mg, Ti, Be, Co |
HCP | <1120> | {1010} | Ti, Mg, Zr, Be |
HCP | <1120> | {1011} | Ti, Mg |
Tres observaciones generales son de gran importancia:
- Las direcciones de deslizamiento siempre son en la dirección de empaquetamiento compacto. Existen excepciones, por ejemplo, mercurio sólido.
- El deslizamiento ocurre usualmente sobre la mayoría de los planos compactos. Esta observación esta relacionada con el hecho de que los planos empaquetados más densamente también son el grupo de planos (hkl) ocupados que tienen el espaciamiento más amplio.
- El deslizamiento se produce primero sobre el sistema de deslizamiento que tiene el mayor esfuerzo de corte a lo largo de su dirección de deslizamiento.
REFERENCIAS
VERHOEVEN, John, D. Fundamentos de Metalurgia Física. Ed. Limusa. 1987
SANDS, Donald. Introducción a la Cristalografía. Ed. Reverté S.A.
SMITH, William F. Fundamentos de la Ciencia e Ingeniería de Materiales. Ed. Mc Graw Hill. 1993
BRICEÑO, Carlos Omar. Química. Ed. Educativa