Características de los Sólidos Cristalinos

Características de los sólidos cristalinos

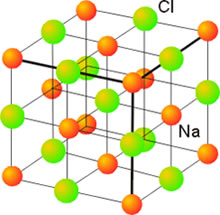
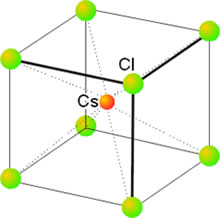
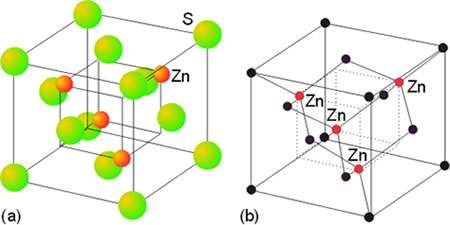
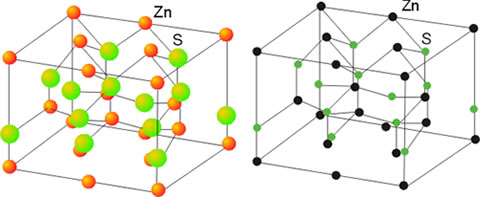
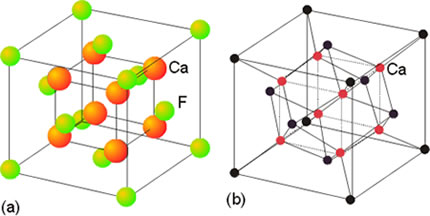
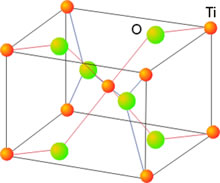
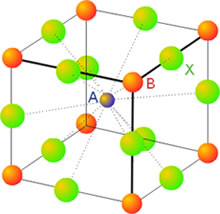
En el estado sólido, las moléculas, átomos o iones que componen la sustancia considerada están unidas entre sí por fuerzas relativamente intensas, formando un todo compacto. La mayor proximidad entre sus partículas constituyentes es una característica de los sólidos y permite que entren en juego las fuerzas de enlace que ordenan el conjunto, dando lugar a una red cristalina. En ella las partículas ocupan posiciones definidas y sus movimientos se limitan a vibraciones en torno a los vértices de la red en donde se hallan situadas. Por esta razón las sustancias sólidas poseen forma y volumen propios.

La mayor parte de los sólidos presentes en la naturaleza son cristalinos aun cuando en ocasiones esa estructura ordenada no se refleje en una forma geométrico regular apreciable a simple vista. Ello es debido a que con frecuencia están formados por un conjunto de pequeños cristales orientados de diferentes maneras, en una estructura policristalina. Los componentes elementales de una red cristalina pueden ser átomos, moléculas o iones, de ahí que no se pueda hablar en general de la molécula de un cristal, sino más bien de un retículo elemental o celdilla unidad, que se repite una y otra vez en una estructura periódica o red cristalina.

Las propiedades físicas de los sólidos, tales como temperatura de fusión, capacidad para conducir la corriente, resistencia a la deformación, dureza, etc., dependen de las características de las fuerzas de enlace que unen las entidades elementales. Así, los sólidos iónicos, como las sales, son duros y a la vez frágiles, con puntos de fusión altos. Aunque son malos conductores de la electricidad sus disoluciones, sin embargo, presentan una conductividad elevada. Los sólidos formados por moléculas apolares, como el Cl2, el H2 o el CO2, son blandos como corresponde a la debilidad de las fuerzas de interacción entre ellas (fuerzas de Van der Waals). Presentan un punto de fusión bajo lo que indica que sólo a bajas temperaturas, las débiles fuerzas ordenadores del enlace pueden predominar sobre el efecto disgregador del calor. Su conductividad eléctrica es extremadamente baja como corresponde a la ausencia de cargas libres.

Los sólidos formados por moléculas polares, como el agua, presentan características intermedias entre ambos tipos de sólidos, los iónicos y los apolares. Las características del enlace metálico con un gas de electrones externos compartidos hace que los sólidos metálicos sean buenos conductores de la electricidad y del calor, y dúctiles y maleables, aunque con elevados puntos de fusión. Un tipo de sólido de propiedades extremas lo constituyen los sólidos covalentes; están formados por una red tridimensional de enlaces atómicos fuertes que dan lugar a propiedades tales como elevados puntos de fusión, escasa conductividad y extraordinaria dureza. El diamante, que es carbono puro cristalizado, constituye un ejemplo de este tipo de sólidos.

Teoría de bandas en los sólidos

Todos los sólidos cristalinos presentan una estructura periódica, por lo que un electrón genérico que se viese sometido a la influencia de la red cristalina poseería una energía potencial que variaría también de una forma periódica en las tres direcciones del espacio. Esta situación se traduce, de acuerdo con la mecánica cuántica, en que cada uno de los niveles de energía que correspondería a un átomo aislado se desdobla tanto más cuanto mayor es el número N de átomos constitutivos de la red, dando lugar a una serie de niveles prácticamente contiguos que en conjunto constituyen una banda de energía.

El número máximo de electrones que pueden ocupar una banda determinada viene limitado por el principio de exclusión de Pauli que indica que en cada nivel atómico se pueden acomodar, a lo más, dos electrones y siempre que sus espines respectivos sean opuestos; por tal motivo en una cualquiera de las bandas correspondientes a una red cristalina formada por N átomos iguales, podrán acomodarse como máximo 2N electrones.

Las bandas de energía en un sólido cristalino desempeñan el mismo papel que los niveles electrónicos de un átomo aislado e incluso se representan de la misma manera mediante las letras s, p, d, f, etc.; por tanto, la energía de un electrón en un sólido sólo puede tomar valores comprendidos en alguna de las múltiples bandas de energía del sólido.

En algunos tipos de sólidos las bandas pueden solaparse y en otros, sin embargo, los correspondientes diagramas de energía aparecen separados por espacios intermedios que representan valores de la energía que no pueden poseer los electrones; por ello se les denomina bandas prohibidas.

La teoría de bandas permite explicar con una excelente aproximación el fenómeno de la conducción eléctrica en los sólidos. En algunos sólidos, la última banda no está ocupada completamente, lo que permite a los electrones de esa banda ganar energía por la acción de un campo eléctrico externo y desplazarse por la red.

La mayor parte de los metales presentan, no obstante, bandas superiores incompletas que se superponen entre sí permitiendo, asimismo, la movilidad de los electrones que son excitados por un campo eléctrico. Este movimiento de cargas en el seno de la red cristalina constituye una corriente eléctrica.

Una gran mayoría tanto de sólidos iónicos como de covalentes, son malos conductores de la electricidad (aisladores). En ellos la banda más alta conteniendo electrones (banda de valencia) está completamente llena.

Ello supone, de acuerdo con el principio de exclusión de Pauli, que los electrones no pueden ganar energía y saltar de un nivel a otro dentro de la banda, lo que equivale a restringir su movilidad al entorno de su núcleo atómico.

Además la siguiente banda vacía (banda de conducción) está lo suficientemente separada de aquélla como para que la banda prohibida no pueda ser salvada por la acción de un campo eléctrico ordinario. Tal circunstancia explica su reducida conductividad eléctrica.

Existen algunos sólidos como el silicio y el germanio que tienen una estructura de bandas semejante a la de los aisladores. Sin embargo, en ellos la banda prohibida que separa la de valencia, completamente llena, y la de conducción, completamente vacía, es estrecha, de modo que es posible excitar los electrones más altos de la banda de valencia y transferidos a la de conducción.

En tal caso se puede hablar tanto de una conducción por los electrones de la banda superior, como de conducción por los huecos que se generan en la banda inferior y que se comportan como cargas positivas. Se trata de sólidos semiconductores. El hecho de que su banda prohibida sea estrecha permite bombear electrones a la banda de conducción sin más que elevar suficientemente la temperatura.

Los semiconductores constituyen los materiales sólidos clave en la fabricación de dispositivos electrónicos. Sus propiedades, mejoradas y aprovechadas gracias a la investigación básica y aplicada, no sólo han constituido un elemento clave en el desarrollo de la informática, la instrumentación científica de alto nivel y las telecomunicaciones, sino también en el diseño de aparatos electrodomésticos y de uso habitual.

Fuente: http://www.salonhogar.com/ciencias/fisica/estados_materia/estado_solido.htm

Mario Pedraza

Electrónica del Estado Sólido Sección 2

Sustancias con Enlace Iónico

Sustancias con Enlace Iónico

Puntos de ebullición y de fusión.

Las sustancias que presentan enlaces iónicos son sólidas a temperatura y presión ambiente pues sus puntos de fusión y ebullición son altos debido a que al encontrarse los iones fuertemente atraídos (como nos referimos en interacciones entre partículas) se requiere mucha energía para poder separarlos y que puedan cambiar de estado. Cuanto mayor es la carga o menor es la distancia entre los iones, más elevados son los puntos de fusión y de ebullición.

Sustancia	Punto de fusión en °C
NaCl	801
BaCl2	963
LiF	845
CaF2	1360

Dureza.

La dureza es la resistencia que ofrecen los sólidos a ser rayados. La propia estructura ordenada de los sólidos iónicos, explica su dureza, ya que no hay lugar hacia donde se desplacen los iones bajo presión. Para rayar un cristal es necesario romper los enlaces entre iones (op.cit. en interacciones entre partículas). La dureza varía desde 1 a 9 en la escala de Mohs.

Escala de Mohs	valor
Talco	1
Yeso	2
Calcita	3
Fluorita	4
Apatito	5
Ortosa	6
cuarzo	7
Topacio	8
Corindón	9
diamante	10

Solubilidad.

Los disolventes polares hacen disminuir las fuerzas atractivas al interponerse las moléculas del disolvente entre los iones. Cada ion se rodea de moléculas de disolvente (solvatación). La solubilidad disminuye si aumenta la carga de los iones. Así las sustancias formadas por metales del grupo II A (alcalinos térreos) son menos solubles que las formadas por metales del grupo I A (alcalinos)

Conductividad.

Las que presentan enlace iónico tienen sus electrones muy bien localizados, es decir que los iones en los cristales carecen de movilidad; sin embargo cuando están fundidos o disueltos en soluciones acuosas, como los iones se encuentran libres, es decir adquieren movilidad, por lo cual conducen la corriente eléctrica y el calor.

Medidor de conductividad video

Fuente: http://www.quimi-red.com.ar/propiedades_sustancias.htm#sustancias_ionicas

Mario Pedraza
Electronica del Estado Sólido Sección 2

Imperfecciones en las Redes

IMPERFECCIONES EN LAS REDES CRISTALINAS
Las imperfecciones se encuentran dentro de la zona de ordenamiento de largo alcance (grano) y se clasifican de la siguiente manera:
DEFECTOS PUNTUALES (puntos defectuosos):
Defectos puntuales: Los defectos puntuales son discontinuidades de la red que involucran uno o quizá varios átomos. Estos defectos o imperfecciones,, pueden ser generados en el material mediante el movimiento de los átomos al ganar energía por calentamiento; durante el procesamiento del material; mediante la introducción de impurezas; o intencionalmente a través de las aleaciones.
Huecos: Un Hueco se produce cuando falta un átomo en un sitio normal. Las vacancias se crean en el cristal durante la solidificación a altas temperaturas o como consecuencia de daños por radiación. A temperatura ambiente aparecen muy pocas vacancias, pero éstas se incrementan de manera exponencial conforme se aumenta la temperatura.
Defectos intersticiales: Se forma un defecto intersticial cuando se inserta un átomo adicional en una posición normalmente desocupada dentro de la estructura cristalina. Los átomos intersticiales, aunque mucho más pequeños que los átomos localizados en los puntos de la red, aún así son mayores que los sitios intersticiales que ocupan; en consecuencia, la red circundante aparece comprimida y distorsionada. Los átomos intersticiales como el hidrógeno a menudo están presentes en forma de impurezas; los átomos de carbono se agregan al hierro para producir acero. Una vez dentro del material, el número de átomos intersticiales en la estructura se mantiene casi constante, incluso al cambiar la temperatura.

Defectos sustitucionales: Se crea un defecto sustitucional cuando se remplaza un átomo por otro de un tipo distinto. El átomo sustitucional permanece en la posición original. Cuando estos átomos son mayores que los normales de la red, los átomos circundantes se comprimen; si son más pequeños, los átomos circundantes quedan en tensión. En cualquier caso, el defecto sustitucional distorsiona la red circundante. Igualmente, se puede encontrar el defecto sustitucional como una impureza o como un elemento aleante agregado deliberadamente y, una vez introducido, el número de defectos es relativamente independiente de la temperatura.

IMPORTANCIA DE LOS DEFECTOS PUNTUALES: Los defectos puntuales alteran el arreglo perfecto de los átomos circundantes, distorsionando la red a lo largo de quizás cientos de espaciamientos atómicos, a partir del defecto. Una dislocación que se mueva a través de las cercanías generales de un defecto puntual encuentra una red en la cual los átomos no están en sus posiciones de equilibrio. Esta alteración requiere que se aplique un esfuerzo más alto para obligar a que la dislocación venza al defecto, incrementándose así la resistencia del material.

DEFECTOS LINEALES (dislocaciones) :

Defectos Lineales (Dislocaciones):

Las dislocaciones son imperfecciones lineales en una red que de otra forma sería perfecta. Generalmente se introducen en la red durante el proceso de solidificación del material o al deformarlo. Aunque en todos los materiales hay dislocaciones presentes, incluyendo los materiales cerámicos y los polímeros, son de particular utilidad para explicar la deformación y el endurecimiento de los metales. Podemos identificar dos tipos de dislocaciones: la dislocación de tornillo y la dislocación de borde.

Dislocación de tornillo:
La dislocación de tornillo se puede ilustrar haciendo un corte parcial a través de un cristal perfecto, torciéndolo y desplazando un lado del corte sobre el otro la distancia de un átomo.
Dislocaciones de borde:
Una dislocación de borde se puede ilustrar haciendo un corte parcial a través de un cristal perfecto, separándolo y rellenando parcialmente el corte con un plano de átomos adicional. El borde inferior de este plano adicional representa la dislocación de borde.
Dislocaciones mixtas:
Las dislocaciones mixtas tienen componentes tanto de borde como de tornillo, con una región de transición entre ambas. El vector de Burgers, sin embargo, se conserva igual para todas las porciones de la dislocación mixta.

IMPORTANCIA DE LAS DISLOCACIONES:

Aunque en algunos materiales cerámicos y polímeros puede ocurrir deslizamiento, el proceso de deslizamiento es de particular utilidad para entender el comportamiento mecánico de los metales.

En primer término, el deslizamiento explica por qué la resistencia de los metales es mucho menor que el valor predecible a partir del enlace metálico. Si ocurre el deslizamiento, sólo es necesario que se rompa en algún momento una pequeña fracción de todas las uniones metálicas a través de la interfase, por lo que la fuerza requerida para deformar el metal resulta pequeña.

Segundo, el deslizamiento le da ductilidad a los metales. Si no hay dislocaciones presentes, una barra de hierro sería frágil; los metales no podrían ser conformados utilizando los diversos procesos, que involucran la deformación para obtener formas útiles, como la forja.

En tercer lugar, controlamos las propiedades mecánicas de un metal o aleación al interferir el movimiento de las dislocaciones. Un obstáculo introducido en el cristal impedirá que en una dislocación se deslice, a menos que apliquemos mayor fuerza. Si es necesario aplicar una fuerza superior, entonces el metal resulta ser más resistente. Estos obstáculos pueden ser defectos puntuales o borde de grano.

En cuarto lugar, se puede prevenir el deslizamiento de las dislocaciones achicando el tamaño de grano o introduciendo átomos de diferente tamaño, que son las aleaciones.

En los materiales se encuentran enormes cantidades de dislocaciones. La densidad de dislocaciones, o la longitud total de dislocaciones por unidad de volumen, generalmente se utiliza para representar la cantidad de dislocaciones presentes. Densidades de dislocación de 10ˆ-6 cm/cm3 son típicas en los metales más suaves, en tanto que se pueden conseguir densidades de hasta 10ˆ-12 cm/cm3 deformando el material.

DEFECTOS PLANARES: (superficies externas y limite de grano)

DEFECTOS DE SUPERFICIE:

Modelo de cristalización en la solidificación de metales La estructura final resultante está constituida por un agrupamiento de granos o cristales de forma irregular pero guardando cada uno una orientación fija y bien determinada.

Los defectos de superficie son las fronteras o planos que separan un material en regiones de la misma estructura cristalina pero con orientaciones cristalográficas distintas, y la superficie externa de un material. En las superficies externas del material la red termina de manera abrupta. Cada átomo de la superficie ya no tiene el mismo número de coordinación y se altera el enlace atómico. Asimismo, la superficie puede ser muy áspera, contener pequeñas muescas y quizá ser mucho más reactiva que el interior del material. En líquidos, los átomos en la superficie tienen mayor energía porque no tienen todos sus átomos vecinos. Esto hace que al tratar de minimizar la energía se tiende a reducir el numero de átomos en esta condición, por lo tanto tienden a reducir la superficie respecto al volumen, esto geométricamente corresponde a una esfera.

CRISTALIZACION El crecimiento de los cristales que se inicia en los centros o núcleos de cristalización en el metal líquido, no puede ser uniforme a causa de los diferentes factores de la composición del metal, la velocidad de enfriamiento y las interferencias que se producen entre ellos mismos durante el proceso de crecimiento.

LIMITES DE GRANO:

La microestructura de la mayor parte de los materiales está formada por muchos granos. Un grano es una porción del material dentro del cual el arreglo atómico es idéntico. Sin embargo, la orientación del arreglo atómico, o de la estructura cristalina, es distinta para cada grano. En la figura se muestran de manera esquemática tres granos; la red de cada uno de ellos es idéntica pero están orientados de manera distinta. La frontera de grano, que es la superficie que separa los granos, es una zona estrecha en la cual los átomos no están correctamente espaciados. Esto quiere decir que, en algunos sitios, los átomos están tan cerca unos de otros en la frontera de grano que crean una región de compresión y en otras áreas están tan alejados que crean una región de tensión.

Los átomos cerca de las fronteras de los tres granos no tienen un espaciamiento o arreglo de equilibrio.

Un método para controlar las propiedades de un material es controlando el tamaño de los granos. Reduciendo el tamaño de éstos se incrementa su número y, por tanto, aumenta la cantidad de fronteras de grano. Cualquier dislocación se moverá solamente una distancia corta antes de encontrar una frontera de grano, incrementando así la resistencia del metal. Se puede relacionar el tamaño de grano con el tensión de fluencia del material. Los limites de grano tienen una influencia importante sobre las propiedades del metal, su numero y tamaño esta en funcion de la tasa de nucleacion y los indices de crecimiento de este. Una vez que el metal se ha solidificado, se puede modificar el tamaño y numero de granos, ya sea por deformacion o tratamiento termico, lo cual permitira que sus propiedades mecanicas varien considerablemente, la siguiente ecuacion muestra su influencia en el esfuerzo de cedencia:

ß = K1 + K2/ D ˆ- 2

Donde ß es el esfuerzo de Cedencia; K1 y K2 ctes del Material; D es el tamaño del Grano

Fuente: http://descom.jmc.utfsm.cl/proi/materiales/ESTRUCTURAS.htm#IMPERFECCIONESENLASREDESCRISTALINAS

Mario Pedraza

Electrónica del Estado Sólido Sección 2

Estructura de los Sólidos

Estructura de los Sólidos

Sólido cristalino. Redes espaciales. Celdillas unidad.

Si los átomos o iones de un sólido están ordenados según una disposición que se repite en las tres dimensiones, forman un sólido que se dice posee estructura cristalina y es referido como sólido cristalino o material cristalino. Ejemplos de materiales cristalinos son los metales, las aleaciones, y algunos materiales cerámicos.

La disposición de los átomos en los sólidos cristalinos se puede representar considerando a los átomos como los puntos de intersección de una red de líneas en tres dimensiones. Esta red se denomina red espacial. Cada punto de la red espacial tiene idéntico entorno. Una red espacial se define especificando la disposición de los átomos en una celdilla unidad que se repite n veces dentro de la red espacial. El tamaño y forma de la celdilla unidad se describe mediante tres vectores a, b y c, con origen en un vértice de la celdilla unidad, tal como se muestra en la figura 1.1. Las longitudes a, b y c y los ángulos α, β, y γ son las constantes reticulares de la celdilla unidad.

(a) Red espacial de un sólido cristalino. (b) Celdilla unidad con indicación de las constantes de red.

Celdillas Unitarias de Bravais

El número de redes espaciales no es infinita. Los cristalógrafos han mostrado que sólo existen siete sistemas cristalinos independientes posibles, que dan lugar a 14 redes espaciales, denominadas redes de Bravais. En la figura se representan las celdillas unidad correspondientes a las 14 redes de Bravais. En la tabla se dan los parámetros de la red necesarios para describir los distintos sistemas cristalinos, que definen el tamaño y la forma de cada celdilla unidad.

Si se analiza la tabla y la figura se observa que hay cuatro sistemas básicos de celdilla unidad: sencilla, centrada en el cuerpo, centrada en las caras y centrada en la base. En el sistema cúbico hay tres tipos posibles de celdilla unidad: cúbica sencilla, cúbica centrada en el cuerpo y cúbica centrada en las caras. En el sistema ortorrómbico hay los cuatro tipos posibles: ortorrómbico sencillo, ortorrómbico centrado en el cuerpo, ortorrómbico centrado en las bases y ortorrómbico centrado en las caras. El sistema tetragonal presenta dos tipos de celdillas posibles, tetragonal sencilla y tetragonal centrada en el cuerpo. El sistema monoclínico tiene celdillas unidad sencilla y centrada en la base. Los sistemas romboédrico, hexagonal y triclínico tienen sólo el tipo sencillo de celdilla unidad.

Clasificación de redes espaciales en sistemas cristalinos

Las 14 celdillas unidad de Bravais agrupadas en sistemas cristalinos

Fuente: http://www.xtec.cat/~maleman1/uned/unedcurset21.html

Mario Pedraza
Electronica del Estado Sólido Sección 2

Solid State Structure

Solid State Structure

In solids, the way the atoms or molecules arrange themselves contributes to the appearance and the properties of the materials.

Atoms can be gathered together as an aggregate through a number of different processes, including condensation, pressurization, chemical reaction, electrodeposition, and melting. The process usually determines, at least initially, whether the collection of atoms will take to form of a gas, liquid or solid. The state usually changes as its temperature or pressure is changed. Melting is the process most often used to form an aggregate of atoms. When the temperature of a melt is lowered to a certain point, the liquid will form either a crystalline solid or and amorphous solids.

Amorphous Solids

A solid substance with its atoms held apart at equilibrium spacing, but with no long-range periodicity in atom location in its structure is an amorphous solid. Examples of amorphous solids are glass and some types of plastic. They are sometimes described as supercooled liquids because their molecules are arranged in a random manner some what as in the liquid state. For example, glass is commonly made from silicon dioxide or quartz sand, which has a crystalline structure. When the sand is melted and the liquid is cooled rapidly enough to avoid crystallization, an amorphous solid called a glass is formed. Amorphous solids do not show a sharp phase change from solid to liquid at a definite melting point, but rather soften gradually when they are heated. The physical properties of amorphous solids are identical in all directions along any axis so they are said to have isotropic properties, which will be discussed in more detail later

.

Crystalline Solids

More than 90% of naturally occurring and artificially prepared solids are crystalline. Minerals, sand, clay, limestone, metals, carbon (diamond and graphite), salts ( NaCl, KCl etc.), all have crystalline structures. A crystal is a regular, repeating arrangement of atoms or molecules. The majority of solids, including all metals, adopt a crystalline arrangement because the amount of stabilization achieved by anchoring interactions between neighboring particles is at its greatest when the particles adopt regular (rather than random) arrangements. In the crystalline arrangement, the particles pack efficiently together to minimize the total intermolecular energy.

The regular repeating pattern that the atoms arrange in is called the crystalline lattice. The scanning tunneling microscope (STM) makes it possible to image the electron cloud associated individual atoms at the surface of a material. Below is an STM image of a platinum surface showing the regular alignment of atoms.

Crystal Structure

Crystal structures may be conveniently specified by describing the arrangement within the solid of a small representative group of atoms or molecules, called the 'unit cell.' By multiplying identical unit cells in three directions, the location of all the particles in the crystal is determined. In nature, 14 different types of crystal structures or lattices are found. The simplest crystalline unit cell to picture is the cubic, where the atoms are lined up in a square, 3D grid. The unit cell is simply a box with an atom at each corner. Simple cubic crystals are relatively rare, mostly because they tend to easily distort. However, many crystals form body-centered-cubic (bcc) or face-centered-cubic (fcc) structures, which are cubic with either an extra atom centered in the cube or centered in each face of the cube. Most metals form bcc, fcc or Hexagonal Close Packed (hpc) structures; however, the structure can change depending on temperature. These three structures will be discussed in more detail on the following page.

Crystalline structure is important because it contributes to the properties of a material. For example, it is easier for planes of atoms to slide by each other if those planes are closely packed. Therefore, lattice structures with closely packed planes allow more plastic deformation than those that are not closely packed. Additionally, cubic lattice structures allow slippage to occur more easily than non-cubic lattices. This is because their symmetry provides closely packed planes in several directions. A face-centered cubic crystal structure will exhibit more ductility (deform more readily under load before breaking) than a body-centered cubic structure. The bcc lattice, although cubic, is not closely packed and forms strong metals. Alpha-iron and tungsten have the bcc form. The fcc lattice is both cubic and closely packed and forms more ductile materials. Gamma-iron, silver, gold, and lead have fcc structures. Finally, HCP lattices are closely packed, but not cubic. HCP metals like cobalt and zinc are not as ductile as the fcc metals.

Fuente: http://www.ndt-ed.org/EducationResources/CommunityCollege/Materials/Structure/solidstate.htm

Mario Pedraza
Electrónica del Estado Sólido Sección 2

Basic Semiconductor Crystal Structure

Basic Semiconductor Crystal Structure

To understand how diodes, transistors, and other semiconductor devices can do what they do, it is first necessary to understand the basic structure of all semiconductor devices. Early semiconductors were fabricated from the element Germanium, but Silicon is preferred in most modern applications.

The crystal structure of pure silicon is of course 3-dimensional, but that is difficult to display or to see, so the image to the left is often used to represent the crystal structure of silicon. For you physics types, silicon (and germanium) falls in column IVa of the Periodic Table. This is the carbon family of elements. The essential characteristic of these elements is that each atom has four electrons to share with adjacent atoms in forming bonds.

While this is an oversimplified description, the nature of a bond between two silicon atoms is such that each atom provides one electron to share with the other. The two electrons thus shared are in fact shared equally between the two atoms. This type of sharing is known as a covalent bond. Such a bond is very stable, and holds the two atoms together very tightly, so that it requires a lot of energy to break this bond.

For those who are interested, the actual bonds in a 3-dimensional silicon crystal are arranged at equal angles from each other. If you visualize a tetrahedron (a pyramid with three points on the ground and a fourth point sticking straight up) with the atom centered inside, the four bonds will be directed towards the points of the tetrahedron.

Now we have our silicon crystal, but we still don't have a semiconductor. In the crystal we saw above, all of the outer electrons of all silicon atoms are used to make covalent bonds with other atoms. There are no electrons available to move from place to place as an electrical current. Thus, a pure silicon crystal is quite a good insulator. In fact, it is almost glass, which is silicon dioxide. A crystal of pure silicon is said to be an intrinsic crystal.

To allow our silicon crystal to conduct electricity, we must find a way to allow some electrons to move from place to place within the crystal, in spite of the covalent bonds between atoms. One way to accomplish this is to introduce an impurity such as Arsenic or Phosphorus into the crystal structure, as shown to the right. These elements are from column Va of the Periodic Table, and have five outer electrons to share with other atoms. In this application, four of these five electrons bond with adjacent silicon atoms as before, but the fifth electron cannot form a bond. This electron can easily be moved with only a small applied electrical voltage. Because the resulting crystal has an excess of current-carrying electrons, each with a negative charge, it is known as "N-type" silicon.

This construction does not conduct electricity as easily and readily as, say, copper or silver. It does exhibit some resistance to the flow of electricity. It cannot properly be called a conductor, but at the same time it is no longer an insulator. Therefore, it is known as a semiconductor.

While this effect is interesting, it still isn't particularly useful by itself. A plain carbon resistor is easier and cheaper to manufacture than a silicon semiconductor one. We still don't have any way to actually control an electrical current.

But wait a moment! We obtained a semiconductor material by introducing a 5-electron impurity into a matrix of 4-electron atoms. (For you physics types, we're only looking at the outer electrons that are available for bonding -- electrons in inner shells are not included in the process or in this discussion.) What happens if we go the other way, and introduce a 3-electron impurity into such a crystal? Suppose we introduce some Aluminum (from column IIIa in the Periodic Table) into the crystal, as shown to the left? We could also try Gallium, which is also in column IIIa right under aluminum. Now what?

These elements only have three electrons available to share with other atoms. Those three electrons do indeed form covalent bonds with adjacent silicon atoms, but the expected fourth bond cannot be formed. A complete connection is impossible here, leaving a "hole" in the structure of the crystal.

Experimentation shows that there is an empty place where an electron should logically go, and often an electron will try to move into that space to fill it. However, the electron filling the hole had to leave a covalent bond behind to fill this empty space, and therefore leaves another hole behind as it moves. Yet another electron may move into that hole, leaving another hole behind, and so forth. In this manner, holes appear to move as positive charges through the crystal. Therefore, this type of semiconductor material is designated "P-type" silicon.

Fuente: http://www.play-hookey.com/semiconductors/basic_structure.html

Mario Pedraza

Electrónica del Estado Sólido Sección 2

Sólidos Iónicos

Los compuestos iónicos suelen presentar una serie de características físicas que los distinguen de los covalentes. Así, los sólidos iónicos como el cloruro sódico y el nitrato de potasio tienen puntos de fusión moderadamente altos y son solubles en disolventes polares, en particular en agua. Sin embargo existen excepciones como el CaF₂ el cual presenta un elevado punto de fusión pero es insoluble en agua. Los compuestos iónicos también presentan una baja conductividad eléctrica en el estado sólido pero se hacen buenos conductores de la electricidad cuando se funden o cuando se disuelven en disolventes polares como el agua.

Los sólidos iónicos presentan estructuras con bajos números de coordinación, a diferencia de los sólidos metálicos, lo que explica su menor densidad. De hecho, la distinción entre un sólido iónico y uno covalente puede establecerse en función del número de coordinación, al que puede llegarse de forma experimental mediante técnicas de difracción de rayos X. Sin embargo, algunos sólidos covalentes como el diamante presentan también bajos números de coordinación, por lo que es necesario un criterio más específico para establecer un sólido como iónico.

La clasificación de un sólido como iónico se basa en la comparación de sus propiedades con las que predice el modelo iónico. Este es un modelo límite del enlace entre átomos y se basa en considerar al sólido formado por una red de esferas cargadas con signos opuestos y que interaccionan entre sí mediante fuerzas de tipo coulombianas. Si los parámetros termodinámicos calculados para el sólido empleando el modelo iónico coinciden con los determinados experimentalmente, entonces el sólido presenta naturaleza iónica. No obstante, hay que indicar que en algunos casos particulares esta coincidencia numérica no implica siempre la existencia de un enlace iónico.

Estructuras Características de los Sólidos Iónicos

Las estructuras que se describen en este apartado son los modelos que describen a un gran número de sólidos iónicos. Por ejemplo, la estructura de la sal de roca, que toma su nombre de la forma mineral del NaCl, es característica de muchos otros sólidos iónicos. Muchas de las estructuras pueden considerarse constituidas por redes formadas por iones positivos y negativos en las que se maximizan las fuerzas atractivas entre iones de signos opuestos y se minimizan las fuerzas repulsivas entre iones de la misma carga.

Estructuras cristalinas modelo de compuestos ionicos

Estructura cristalina	Ejemplo
Antifluorita	K2O, K2S,Li2O, Na2O, Na2Se, Na2S
Cloruro de cesio	CsCl, CaS, TlSb, CsCN, CuZn
Fluorita	CaF2, UO2, BaCl2, HgF2, PbO2
Arseniuro de níquel	NiAs, NiS, FeS, PtSn, CoS
Perovskita	CaTiO3, BaTiO3, SrTiO3
Sal de roca	NaCl, LiCl, KBr, RbI, AgCl, AgBr, MgO, CaO, TiO, FeO, NiO, SnAs, UC, ScN
Rutilo	TiO2, MnO2, SnO2, WO2, MgF2, NiF2
Blenda	ZnS, CuCl, CdS, HgS, GaP, InAs
Wurtzita	ZnS, ZnO, BeO, MnS, AgI, AlN, SiC, NH4F

La estructura del cloruro sódico

Esta estructura está basada en un empaquetamiento cúbico compacto (centrado en las caras) de los aniones y en el que los cationes ocupan todos los huecos octaédricos. La interpretación opuesta es igualmente válida: estructura de empaquetamiento compacto de cationes con los aniones ocupando los huecos octaédricos. En cada celda unidad los iones de un tipo ocupan los vértices y los centros de las caras del cubo mientras que los de signo contrario se sitúan en los centros de las aristas y en el centro del cubo (Figura 6). Cada ion de un signo está rodeado de 6 iones de signo contrario, por lo que el número de coordinación del catión y del anión en este tipo de estructura de 6. Se dice que la estructura presenta coordinación (6,6), donde el primer dígito representa el número de coordinación del catión y el segundo el del anión. Los seis iones de signo contrario que rodean a un ion central se disponen en forma octaédrica. Este tipo de estructura es adoptada por la mayoría de los haluros alcalinos como los de Li, Na, K, Rb y el CsF. También es adoptada por los óxidos de Mg, Ca, Sr, Ba y Cd.

Estructura del NaCl

La estructura del cloruro de cesio

Esta estructura es menos común que la del cloruro de sodio y la presentan los compuestos como el CsCl, CsBr y CsI, así como otros compuestos formados por iones de radios similares a estos como los haluros de amonio (excepto el NH₄Br). La estructura del cloruro de cesio presenta una celda unidad cúbica en la que cada vértice está ocupado por el anión y el centro del cubo se ocupa por el catión, o viceversa (Figura 7) (o viceversa), lo que conduce a una coordinación (8,8).

Estructura del CsCl

Las estructuras de la blenda y de la wurtzita (ZnS)

El sulfuro de cinc cristaliza en dos formas polimórficas, la wurtzita y la blenda. La primera se basa en un empaquetamiento hexagonal de los aniones en el que los cationes ocupan la mitad de los huecos tetraédricos. La estructura de la blenda está basada en un empaquetamiento de los aniones de tipo cúbico centrado en las caras en el que los cationes ocupan la mitad de los huecos tetraédricos. En ambos tipos de estructuras se da la coordinación (4,4). Las dos estructuras se presentan en los óxidos y sulfuros de los metales divalentes como el Be, Zn, Mn, Cd, Hg.

Estructura de la blenda

Estructura de la wurtzita

La estructura de la fluorita (CaF₂)

Esta estructura toma su nombre del mineral fluorita, CaF₂. Consiste en un empaquetamiento cúbico centrado en las caras de los cationes Ca²⁺ en el que los aniones F^- ocupan todos los huecos tetraédricos. La estructura de tipo antifluorita presenta una disposición de cationes y aniones inversa a la de la fluorita. En la estructura de tipo fluorita, los aniones están rodeados de 4 cationes vecinos dispuestos en un entorno tetraédrico. Los cationes están rodeados de 8 aniones que se disponen en un entorno cúbico. Por lo tanto, los números de coordinación para el catión y el anión son diferentes, 8:4 respectivamente, consistente con la estequiometría del compuesto (hay doble número de aniones que de cationes). Este tipo de estructura la presentan los fluoruros de Ca, Sr, Ba, Cd, Hg(II), Pb(II).

Figura 9. Estructura del CaF₂.

La estructura del rutilo (TiO₂)

Toma su nombre del mineral rutilo, un mineral de óxido de Ti(IV). Se basa en un empaquetamiento hexagonal compacto de los aniones en el que los cationes ocupan la mitad de los huecos octaédricos. Cada átomo de Ti está rodeado de seis átomos de oxígeno (disposición octaédrica) y cada átomo de oxígeno se rodea de tres átomos de titanio (disposición trigonal), de forma que la estructura de tipo rutilo presenta coordinación de 6:3. Esta estructura es la adoptada, entre otros, por el óxido de Sn(IV) o casiderita, el MnO₂ y el WO₂ y por los fluoruros del tipo MgF₂ y NiF₂.

Estructura del TiO2 (rutilo)

La estructura de tipo perovskita

El mineral perovskita CaTiO₃ posee una estructura que es el prototipo de muchos sólidos de composición ABX₃, particularmente óxidos. En su forma idealizada, la estructura de perovskita es cúbica, con los átomos A ocupando el centro del cubo y rodeado de 12 átomos de tipo X y los átomos B ocupando los vértices del cubo y rodeado por 6 átomos de tipo X. La suma de las cargas de los iones positivos A y B debe ser de 6 (A²⁺ B⁴⁺, A³⁺ B³⁺,...). La estructura de tipo perovskita está relacionada con la de materiales que presentan propiedades eléctricas muy interesantes como los sólidos piezoeléctricos, ferroeléctricos y los superconductores de alta temperatura.

Estructura de la perovskita.

Fuente: http://www.textoscientificos.com/quimica/inorganica/enlace-ionico/solidos-ionicos

Mario Pedraza

Electrónica del Estado Sólido Sección 2

Bravais Lattices

The fourteen Bravais lattices

There are fourteen distinct space groups that a Bravais lattice can have. Thus, from the point of view of symmetry, there are fourteen different kinds of Bravais lattices.
Auguste Bravais (1811-1863) was the first to count the categories correctly.

The Seven Crystal Systems

I list below the seven crystal systems and the Bravais lattices belonging to each.

---

Cubic (3 lattices)

The cubic system contains those Bravias lattices whose point group is just the symmetry group of a cube. Three Bravais lattices with nonequivalent space groups all have the cubic point group. They are the simple cube, body-centered cubic, and face-centered cubic.

Tetragonal (2 lattices)

The simple tetragonal is made by pulling on two opposite faces of the simple cubic and stretching it into a rectangular prism with a square base, but a height not equal to the sides of the square. By similarly stretching the body-centered cubic one more Bravais lattice of the tetragonal system is constructed, the centered tetragonal.

Orthorhombic (4 lattices)

The simple orthorhombic is made by deforming the square bases of the tetragonal into rectangles, producing an object with mutually perpendicular sides of three unequal lengths. The base orthorhombic is obtained by adding a lattice point on two opposite sides of one object's face. The body-centered orthorhombic is obtained by adding one lattice point in the center of the object. And the face-centered orthorhombic is obtrained by adding one lattice point in the center of each of the object's faces.

Monoclinic (2 lattices)

The simple monoclinic is obtained by distorting the rectangular faces perpendicular to one of the orthorhombic axis into general parallelograms. By similarly stretching the base-centered orthorhombic one produces the base-centered monoclinic.

Triclinic (1 lattice)

The destruction of the cube is completed by moving the parallelograms of the orthorhombic so that no axis is perpendicular to the other two. The simple triclinic produced has no restrictions except that pairs of opposite faces are parallel.

Trigonal (1 lattice)

The simple trigonal (or rhombohedral) is obtained by stretching a cube along one of its axis.

Hexagonal (1 lattice)

The hexagonal point group is the symmetry group of a prism with a regular hexagon as base. The simple hexagonal bravais has the hexagonal point group and is the only bravais lattice in the hexagonal system.

Fuente: http://phycomp.technion.ac.il/~sshaharr/intro.html

Mario Pedraza

Electrónica del Estado Sólido Sección 2

Imperfecciones Cristalinas

Imperfecciones Cristalinas

La Teoría Cristalina se basa en tres importantes postulados, son estos:

- Postulado Reticular; el cristal es un medio periódico infinito definido por una de las catorce redes de Bravais.

- Postulado estructural; el cristal posee una estructura atómica y la simetría de esta corresponde a uno de los 230 grupos espaciales ( 32 clases de simetría puntual + 14 redes de Bravais)

- Postulado energético; los atomos en la estructura cristalina ocupan posiciones de equilibrio para los cuales la energía es mínima.

Por todo esto, la teoría cristalina nos proporciona una idea del cristal donde el orden, existe, manda, en todo momento. Pero la realidad es muy distinta, el cristal real no es un ente atómico perfecto, sino que esta lleno de defectos. Por ejemplo, un cristal de Fluorita se origina por la aposición de miles de millones de átomos, y en este proceso es muy posible que se generen errores en su estructura. Estos errores son los que hacen que cada especimen mineral sea único e irrepetible. Estas imperfecciones son una característica esencial del cristal. Pero solo puede existir un número finito de imperfecciones en el cristal ya que de lo contrario dejaría de ser un sólido cristalino.

Tipos de imperfecciones en los cristales:

- Relativas a su extensión:

La primera imperfección del cristal es su propia limitación, la teoría cristalina considera que la materia cristalina es un medio periódico infinitamente extendido en las tres direcciones del espacio. Pero un cristal real esta limitado en el espacio por caras, por otros cristales adyacentes, o por otros materiales. Por ejemplo un cristal de fluorita puede crecer en una grieta de roca caliza, la estructura de la fluorita se ve limitada en ese caso por la caliza.

En las caras de los cristales existe un estado de no saturación, por ello tiene tendencia a absorber partículas creando por ejemplo epitaxias o películas orientadas. (Definición de epitaxia: es el crecimiento de cristales de un mineral en una cara cristalina de otro mineral (puede darse entre minerales iguales, homoepitaxia), de forma que el sustrato cristalino de ambos minerales tiene la misma orientación estructural. Existe, homoepitaxia o heteroepitaxia según los materiales sean iguales o distintos.

- Relativas a su composición:

Los minerales no suelen ser sustancias puras, un mineral puro es algo excepcional. La mayoría presenta una variación en su composición química.

Es determinante en la estructura del cristal el tamaño de las partículas que la forman, la coordinación de estas dependen de reglas geométricas fijas.

Sustitución: átomos de igual o parecido tamaño pueden jugar un papel idéntico en la estructura, la geometria no se altera pero la periodicidad si. Existen minerales en la naturaleza con mayor capacidad para aceptar en su estructura otros elementos que no son los que teoricamente tiene su composición básica. Por ejemplo, un mineral muy común, la calcita (Co3Ca), si su composición es pura, es incolora, pero suele tener colores muy diferentes debido a que su composición básica puede variar, dependendiendo de las condiciones en la que crezca, si alrededor existe manganeso, atomos de este elemento se introducen en la estructura de la calcita, sustituyendo atomos de Calcio. En ciertos casos, los nuevos átomos que entran sustituyendo a otros tienen valencia distinta y como el cristal debe de permanecer neutro, la solución es no ocupar todas las posiciones atómicas ocupadas por el ión o atomos de carga menor, esto es lo que se llama lugares vacantes.

Si el átomo que se incorpora a la estructura es muy pequeño puede situarse, sin alterarla profundamente, en los espacios interatómicos existentes, llamados lugares intersticiales.

Las impurezas del medio pueden ser englobadas por el cristal que crece, a estas impurezas se las llama inclusiones. Por ejemplo, no es raro que el cuarzo tenga cristales de otro mineral dentro de él. Un caso muy vistoso son los cristales de cuarzo en la mina Panasqueira en Portugal, donde los cuarzos pueden contener cristales de apatito, arsenopirita, ferberita, turmalina, etc.

- Relativas a su integridad estructural:

El cristal ideal requiere una continuidad perfecta de la red cristalina. La integridad estructural del cristal sufre cuando se rompe esta continuidad de la red. Las imperfecciones más importantes que afectan a la continuidad de una red son las dislocaciones. Las imperfecciones que tiene un cristal real hacen aumentar su energía, pero este tiende a configurarse de la forma más estable posible, es decir con las mínimas imperfecciones. El cristal ideal tiene una estructura cuya energía es mínima. Como la eliminación total de imperfecciones es imposible las concentra en regiones de su estructura y adyacentemente a estas regiones mal formadas estan otras bien formadas. Esta es una idea a la que se llegó gracias a la aplicación de los rayos-X al estudio de los cristales.

- Relativas a su dinámica:

El cristal es un medio dinámico y su entorno, la naturaleza, también lo es, y como tal puede sufrir procesos de corrosión, meteorización, cambios de fase (polimorfismo).

El polimorfismo es una característica de algunas sustancias o elementos químicos para cristalizar en más de un tipo de estructura. Las diferentes estructuras que puede crear una misma sustancia o elemento se llaman formas polimorfas o polimorfos. Por ejemplo el elemento C puede dar, según las condiciones existentes, dos minerales el grafito y el diamante. La sustancia SiO2 puede dar cuarzo bajo, cuarzo alto, tridimita alta, cristobalita alta, coesita y estisovita. Y todas tienen un grupo espacial distinto. Son minerales diferentes pero tienen la misma fórmula química.

Dimensiones de los defectos cristalinos

Defectos puntuales, un lugar vacante en una estructura que afecta a solo un átomo. La introducción de impurezas en una estructura no representa un cambio importante en ella , ya que las impurezas entran en cantidades muy pequeñas y solo producen alteraciones locales sin efectos importantes en la estructura general.

Isomorfismo: hay particulas que forman estructuras de igual dimensión y geometría pero cuya composición química es distinta.

Defectos lineales, dislocaciones, afecta a una serie lineal de átomos. Una dislocación es una discontinuidad en la estructura a lo largo de una fila reticular.

Defectos bidimensionales, son el resultado de una anomalía en un plano reticular. La cara de un cristal es un defecto bidimensional ya que la condición de no saturación de las valencias de los átomos que la forman, hace que se introduzcan efectos que la distinguen del resto del cristal. Los defectos bidimensionales más importantes son los defectos de apilamiento se definen como irregularidades en la secuencia de planos atómicos en una estructura. Estas irregularidades pueden aparecer solo en determinadas circunstancias o bien aparecer siempre en determinados compuestos, por ejemplo el grupo de las micas, cuando esto ocurre la secuencia "anómala" pero común a estos compuestos se denomina politipo y al fenómeno politipismo. Es una variedad especial de polimorfismo. La esfalerita (ZnS) y su polimorfo la wurtzita (ZnS) es un caso de politipismo. Los iones (s2-) en la esfalerita poseen un empaquetamiento cúbico compacto mientras que en la wurtzita poseen un empaquetamiento hexagonal compacto.

Defectos tridimensionales, la mayor parte son inclusiones que rompen la continuidad del cristal en una parte.

Fuente: http://www.spanishminerals.com/Article;%20Imperfecciones%20cristalinas.htm

Mario Pedraza

Electrónica del Estado Sólido Sección 2

Propiedades de los Semiconductores

Propiedades de los Semiconductores

Una propiedad importante en los semiconductores es que posibilita el poder modificar su resistividad de manera controlada entre márgenes muy amplios. La razón primera de este comportamiento diferente reside en su estructura atómica, básicamente en la distancia interatómica de sus átomos en la red así como el tipo de enlace entre ellos.

Así el enlace atómico depende del número de electrones de valencia de los átomos formantes del enlace y de la electronegatividad de los mismos. Los electrones de la capa externa o electrones de valencia son los que determinan y forman los enlaces y los que en su momento pueden determinar el carácter conductivo o no de él. En un semiconductor formado por dos elementos químicos diferentes (Arseniuro de Galio) la asimetría conlleva en general una cierta pérdida de carácter covalente puro, en el sentido de desplazar el centro de gravedad de la carga hacia uno u otro átomo. El parámetro que determina este desplazamiento es la electronegatividad de los átomos constituyentes. Cuanto más diferente sea, mayor será el desplazamiento y el enlace será más iónico que covalente.

La estructura cristalina de los semiconductores es en general compleja aunque puede visualizarse mediante superposición de estructuras más sencillas. La estructura más común es la del diamante, común a los semiconductores Si y Ge, y la del Zinc-Blenda que es la del Arseniuro de Galio. En estas redes cristalinas cada átomo se encuentra unido a otros cuatro mediante enlaces covalentes con simetría tetraédrica. Se requiere que posean unas estructuras cristalinas únicas, es decir, que sea monocristal. Dependiendo de cómo se obtengan éste puede presentarse en forma de monocristal, policristal y amorfo. El comportamiento electrico de los materiales semiconductores (resistividad y movilidad) así como su funcionamiento depende de la estructura cristalina del material de base, siendo imprescindible la forma monocristalina cuando se requiere la fabricación de circuitos integrados y dispositivos electroópticos (láser, leds).

En lo referente al transporte de carga en semiconductores el fenómeno de las colisiones de los portadores con otros portadores, núcleos, iónes y vibraciones de la red, disminuye la movilidad. Ello guarda relación con el parametro de la resistividad (o conductividad) definido como la facilidad para la conducción eléctrica, depende intrínsecamente del material en cuestión y no de su geometria. Así pues en los fenómenos detransporte en semiconductores y a diferencia de los metales, la conducción se debe a dos tipos de portadores, huecos y electrones.

Fuente: http://www.arqhys.com/construccion/semiconductores-propiedades.html

Mario Pedraza
Electrónica del Estado Sólido Sección 2