Crystals have been studied using x-rays, which excite signals from the atoms. The signals are of different strengths and depend on the electron density distribution about atomic cores. Light atoms give weaker signals and hydrogen is invisible to x-rays. However, the mutual atomic arrangements that are called crystal structures can be derived once the chemical formulas and physical densities of solids are known, based on the knowledge that atomic positions are not arbitrary but are dictated by crystal symmetry, and that the diffraction signals received are the result of systematic constructive interference between the scatterers within the regularly repeating internal unit of pattern.SeeCrystallography, Polymorphism (crystallography), X-ray crystallography, X-ray diffraction
Crystals are defined in terms of space, population, and mutual arrangement. Crystal space is represented as an indefinitely extended lattice of periodically repeating points. The periodicity of the lattice is defined by the lengths and mutual orientations of three lattice vectors that enclose the pattern. Population is defined as the total number and kind of fundamental units of structure that form the pattern. The order and periodicity of crystals must extend to about 100 nanometers in all three dimensions of space to give the sharply defined diffraction signals required for mapping structural details by x-rays. Intermediate states of order are seen in liquid crystals, which have long molecules as fundamental units of structure. These are arranged with their lengths parallel to each other, but without periodicity, in the nematic state. In the smectic state there is orientation in equally spaced planes but no sideways periodicity, like traffic moving freely on a multilane highway.
In reality crystal space is not, in general, perfect. The growth process is characterized by constraints and turbulences, and by the dynamic interaction between the crystal and its environment. The process is reflected within the structures formed as an assemblage of atoms is collected and made relatively immobile by releasing the energy known as the heat of crystallization. The resulting crystal lattices resemble a mosaic of slightly misaligned adjacent regions. This is fortunate for research in x-ray crystallography. Perfect alignment would result in subtraction of energy by interference with the primary beam, due to a 180° phase reversal of the reflected beam (primary extinction). Internally diffracted beams would also be attenuated by internal reflection from regions above them (secondary extinction). See Crystal growth
Each of the spatially misaligned mosaic blocks of a single crystal is assumed to maintain lattice periodicity within it. This assumption is confirmed by the sharp diffraction patterns observed. There are some "wrong" atoms, vacant lattice sites, trapped gas atoms, and so forth, and the atomic occupants jiggle about while also vibrating cooperatively and synchronously in complex internal modes of motion. Intricate patterns of electron exchange are enacted, and systematic changes in spin orientations can occur for an atom with a magnetic moment. Details like these are important for understanding the relationships between structure determination on the atomic and molecular levels and the cooperative behavior that determines bulk properties and functions. See Crystal defects, Lattice vibrations
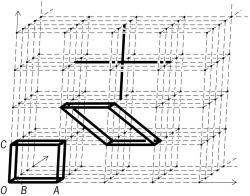
A rectangular space lattice with two possible cells is outlined in the illustration. These have the same cell volumes but different symmetries. Since crystallographic unit cells are completely defined by three lattice vectors, the crystal symmetry referenced to this lattice can be no higher than orthorhombic: a ≠ b ≠ c (OA ≠ OB ≠ OC), and all angles equal to 90°. This and a possible monoclinic cell, with the same vectors a and b (OA and OB) and one angle not equal to 90°, are outlined. If the OAB plane is rotated and the vector a (OA) is extended to terminate at the next lattice point, then all angles differ from 90° and the crystal symmetry represented becomes triclinic. The mutual arrangement and atom coordinates of the cell population must be such that the environment, seen from every point of the space lattice, remains the same.
)
A space lattice, two possible unit cells, and the environment of a point
Space groups are indefinitely extended arrays of symmetry elements disposed on a space lattice. A space group acts as a three-dimensional kaleidoscope: An object submitted to its symmetry operations is multiplied and periodically repeated in such a way that it generates a number of interpenetrating identical space lattices. Space groups are denoted by the Hermann-Mauguin notation preceded by a letter indicating the Bravais lattice on which it is based. For example, P 212121 is an orthorhombic space group; the cell is primitive and three mutually perpendicular screw axes are the symmetry elements. J. D. H. Donnay and D. Harker have shown that it is possible to deduce the space group from a detailed study of the external morphology of crystals.
In general, metallic structures are relatively simple, characterized by a close packing and a high degree of symmetry. Manganese, gallium, mercury, and one form of tungsten are exceptions. A characteristic of metallic structures is the frequent occurrence of allotropic forms; that is, the same metal can have two or more different structures which are most frequently stable in a different temperature range. The forces which link the atoms together in metallic crystals are nondirectional. This means that each atom tends to surround itself by as many others as possible. This results in a close packing, similar to that of spheres of equal radius, and yields three distinct systems: close-packed (face-centered) cubic, hexagonal close-packed, and body-centered cubic.
Simple crystal structures are usually named after the compounds in which they were first discovered (diamond or zinc sulfide, cesium chloride, sodium chloride, and calcium fluoride). Many compounds of the types A+X- and A2+X2- have such structures. They are highly symmetrical, the unit cell is cubic, and the atoms or ions are disposed at the corners of the unit cell and at points having coordinates that are combinations of 0, 1, ½, or ¼.
The sodium chloride structure is an arrangement in which each positive ion is surrounded by six negative ions, and vice versa. The centers of the positive and the negative ions each form a face-centered cubic lattice. Systematic study of the dimensions of the unit cells of compounds having this structure has revealed that:
- 1. Each ion can be assigned a definite radius. A positive ion is smaller than the corresponding atom and a negative ion is larger.
- 2. Each ion tends to surround itself by as many others as possible of the opposite sign because the binding forces are nondirectional.
In the cesium chloride structure each of the centers of the positive and negative ions forms a primitive cubic lattice; the centers are mutually shifted. Contact of the ions of opposite sign here is along the cube diagonal. In the diamond structure, each atom is in the center of a tetrahedron formed by its nearest neighbors. The 4-coordination follows from the well-known bonds of the carbon atoms.
The calcium fluoride structure is divided into eight equal cubelets, calcium ions are situated at corners and centers of the faces of the cell. The fluorine ions are at the centers of the eight cubelets.
Jose Galviz EES
http://encyclopedia2.thefreedictionary.com/Crystal+lattice+structure
No hay comentarios:
Publicar un comentario